But first…
Let’s assume you have a practical (or existential…) need to build some instrument. Your approach may be to look through the junk bin, find some parts that “work”, put them together over an afternoon, and have an instrument that “works”. Or you could look through the literature, reverse-engineer existing devices, model and simulate the various systems, design for production, test and troubleshoot prototypes, argue with the marketing team over the datasheet specs and costs, et cetera, and have an instrument that “works”. There is a spectrum from jank to professional, and the depth of the rabbit hole you go down is arbitrary. Any point on the spectrum is valid for your definition of “works”, if your device meets its implicit or explicit design criteria. But first, you have to know what you are asking your instrument to do.
What am I asking of my densitometer and how can I specify these requirements? I can begin from a set of practical functions and features I would like the instrument to have:
It must measure the local optical density of black-and-white film sheets up to 20x30 cm in size
It must measure density in such a way that the measurement is useful for enlarger and contact printing
It must measure the relative local light intensity of incident light
It must provide a digital readout of density and relative intensity in standard units - O.D. and stops/zones
It must provide an accurate and precise measurement over the range of densities normally encountered in practical photography. The explicit values of accuracy and precision are TBD.
It must allow an automatic zeroing of the readout
It must provide for calibration against a standard
It must be modular, allowing reconfiguration and add-on functionality, such as color and reflection density measurements
It must allow for easy operation
I also found it useful to consider what I’m not asking from my design:
It doesn’t have to be lightweight or especially portable, as it will be a bench instrument
It doesn’t have to be programmable or microcontroller-driven
It doesn’t have to be battery-powered or especially energy efficient
It doesn’t have to be designed for manufacture, as this is a one-off
It doesn’t have to be designed for aesthetics (although style points count)
I’ve tried to list my requirements in decreasing priority, but at this point, they remain somewhat arbitrary choices that should help guide the design. I can look at each statement, expand its meaning, and see how it can be practically solved. Any ambiguous definitions imply that I don’t know the answer straight away. For example, “local” means over a small area, but how small? Is it a percentage of the overall image area, would that make sense? Or is it a fixed area, much smaller than the image dimensions, but greater than the grain size of the image, so that the graininess of the film doesn’t affect it? Ambiguity is generally bad, but not knowing about it is worse. I can at least account for it in the design
Bit first²…
Parts I and II of this article were written by me somewhere at the end 0f 2018, when I had finished the first iteration of the electronics of the instrument and had a plan for the final design. Yet, once again, time happened, five years of it. From the binder in front of me, filed with pages of handwritten text for this series, I can see I had a plan for the structure and development of this narrative. This plan is incomplete and I once again do not know how I will finish it. It is interesting how this project rears its face every other year or so, even as a finished, rather elegant, device, on which I have spent hundreds of hours and dollars. In hindsight, it is in a sense a reflection of my development as an engineer and designer.
As we inch closer to the second half of the third decade of this century, I believe it is time that these texts be made public. I have therefore decided to retain the initial two parts “as-is”, since I like to keep them as a historical snapshot into my thinking at the time. However, the remained of this series will be written in “present time”, sometime in early 2024. I plan to make up the concepts and order as I go along, much like the in-vogue LLMs write their sentences one word at a time. Perhaps I can sound as convincing as some of them. To keep myself out of an endless editorial and conceptual loop, I intend to stick to several basic goals:
present an understandable concept of densitometry and photographic sensitometry in general (as a companion article), which ought to have practical value to interested photographers
present the optical, mechanical, and electrical design of the densitometer and how it evolved by research, trial-and-error, and design choices
discuss future plans and how they may be implemented
discuss details of the design and build that I view as useful information, which is not directly pertinent to the instrument itself
With that in mind, let’s see what we can learn about optics…
What is optical density, anyway?
All of photography is about manipulating light. We bend, diffract, mask and convert light in order to arrive at the negatives, prints, and projections of a desired image. So let’s briefly look at the very basic behavior of light when it encounters an object. In a general sense, a beam of light incident on an object of some finite dimension will look like this:
The beam of light has three options: reflect from the surface, enter the object and be absorbed (converted to heat), or pass through the object (be transmitted). Depending on the material, this light might be scattered, refracted, absorbed and re-emitted by fluorescence, its polarization may change, and undergo a myriad other fantastic processes. For our purposes, we will ignore spectral and polarization considerations and only think of light as some amount of photons per second passing though an area. This is known as flux and we can now have a more specific schematic:
behavior of light passing though a non-opaque object
We can now use notation that defines and accounts for the processes of reflection, absorption, and transmission. For the purposes of explaining optical density, I’ve used i to mean “incident” flux or influx, e to mean “emergent” flux or efflux and r to mean “reflected” flux , aka reflected efflux. Specular and diffuse are a sort of angular definition, specular meaning “light in the original direction” and diffuse meaning “light in a scattered direction”, i.e. diffused by the sample. For example, a mirror is an ideal specular reflector, redirecting incident light at the exact same angle as it fell on it, whereas a white sheet of paper or a slab of plaster is a diffuse reflector, because it will scatter a beam of light in every direction.
From these three quantities, we can describe two basic properties relevant to photography:
Transmission defines how transparent a sample is in terms of the ratio of incident to transmitted light flux (or intensity). A glass slide will have T approaching 1, a blank piece of film will perhaps transmit 50-70% of the light (T=0.6-0.7), and a fully exposed piece of film might only transmit 0.1% of light (T=0.001). Certain filters used in optics and photography may only allow 1/1000000th of the light to pass through.
Reflection, respectively defines how well a surface reflects light as the ratio of reflected to incident light, and R is also in the range of 0 to 1, or 0 to 100%. A mirror will have R approaching 1, a sheet of white paper or fixed-out photo paper will reflect about 90% of incident light, and the darkest areas of a glossy silver-gelatin print will perhaps reflect less than 1% of the light. Some of the darkest known materials, such as Vantablack may only reflect 0.1% of the light or even less, but in real-life terms, reflection coefficients rarely go below 0.001.
In photographic theory, it is customary to express these quantities as their logarithms. This is because a lot of chemical and physical processes, including exposure, development, and the way humans perceive light, exhibit exponential or logarithmic behavior. It also saves us from writing a lot of zeros and transforms multiplication and division into addition and subtraction.
It is here that optical density (OD) emerges:
It is customary to note transmission density with a singular D or OD, while reflection density receives a subscript R. Density can be perceived as the amount of light attenuation during reflection and transmission, or how dark an object appears by transmitted or reflected light. Of our examples, the glass slide would have a D approaching 0, the film may have D=0.15-0.3 when blank and D=3 when exposed and developed. Similarly, photo paper’s Dʀ may be around 0.05 when unexposed and fixed and approaching 2-2.2 when fully exposed and developed. In general, in photography, we deal with transmission densities between 0.05 and 2.5-3, and a normally exposed negative will have a density range (meaning the difference between its minimum density Dmin and its maximum density Dmax) of about 0.8-1.2. Likewise, reflection densities rarely go above 2.2-2.3 in the ideal case, meaning that most prints will have a reflection density range of about 1.8-2.
Philosophically, it’s interesting to think of the compressive force of photography, the ability to distill a situation, an event, an epoch, into a single still image through the use of composition, exposure, and timing. This notion of compression is evident also in the purely technical aspect of taking a photograph: a real-world scene may have dark shadows and dazzling highlights, often in the range of 12 stops or more (equivalent to a log10 range of >3.5, a ratio of 1:4000+), which, when captured on a silver-gelatin negative and then reproduced as a silver-gelatin or alternative photographic print, must represent those 12+ stops with only about 6-7 (Dʀ 1.8-2.1). I discuss this transformation further in a separate article on sensitometry.
But back to density…
Although we have now a definition of density and a rough idea of what it means, there is at least one more specification to be made in the pursuit of a means to measure density. From the definition so far, we can anticipate that a densitometer has a way to measure the flux or intensity of a beam of light and compare that to a reference, take the ratio and it’s logarithm to output a number in terms of density. We know that if we want transmission density, we will measure transmitted light, and for reflection density, it we must quantify the reflected light.
But which light? How do we shine the light through or at a sample, and how do we collect the produced beam before measuring it. We must have a geometrical definition of density and we must think how that definition is interpreted in terms of real-life applications - printing and viewing prints. Making that definition also brings us a step closer to designing an instrument, whose output we can confidently share and compare to other professional or custom-built densitometers.
ANSI ANTICS
Up until the advent of digital photography, everyone had to rely on the chemical process of capturing images, which is inherently sensitive to a LOT of variables. So, as photographic science and engineering advanced, the photographic process became more and more defined and standardized. Film sized were standardized. Film speeds were defined and the methods to test them defined. The whole system of exposure calculation was clarified and defined, so any 100 ASA film could go into any camera set to 100 ASA and produce the same results. It is no surprise then that a plethora of standards exists to define sensitometry and densitometry. In particular, we are interested in ANSI PH/IT 2.18-22 or ISO 5-1 thu 5.
On a side note, I have lost many hours hunting down all the relative standards, even going as far as purchasing some older revisions, in the hope that they will have thorough enough descriptions to base my densitometer design on. That is not the case - these documents are more prescriptive than descriptive and in the end only provide abstract definitions. Nevertheless, the tl;dr when it comes to densitometry can be summarized by a few geometric definitions, several material requirements, and some spectral considerations.
Distilling the standard for transmission density yields the following:
ISO/DIN 5-2 Geometric Requirements for Transmission Density Measurement
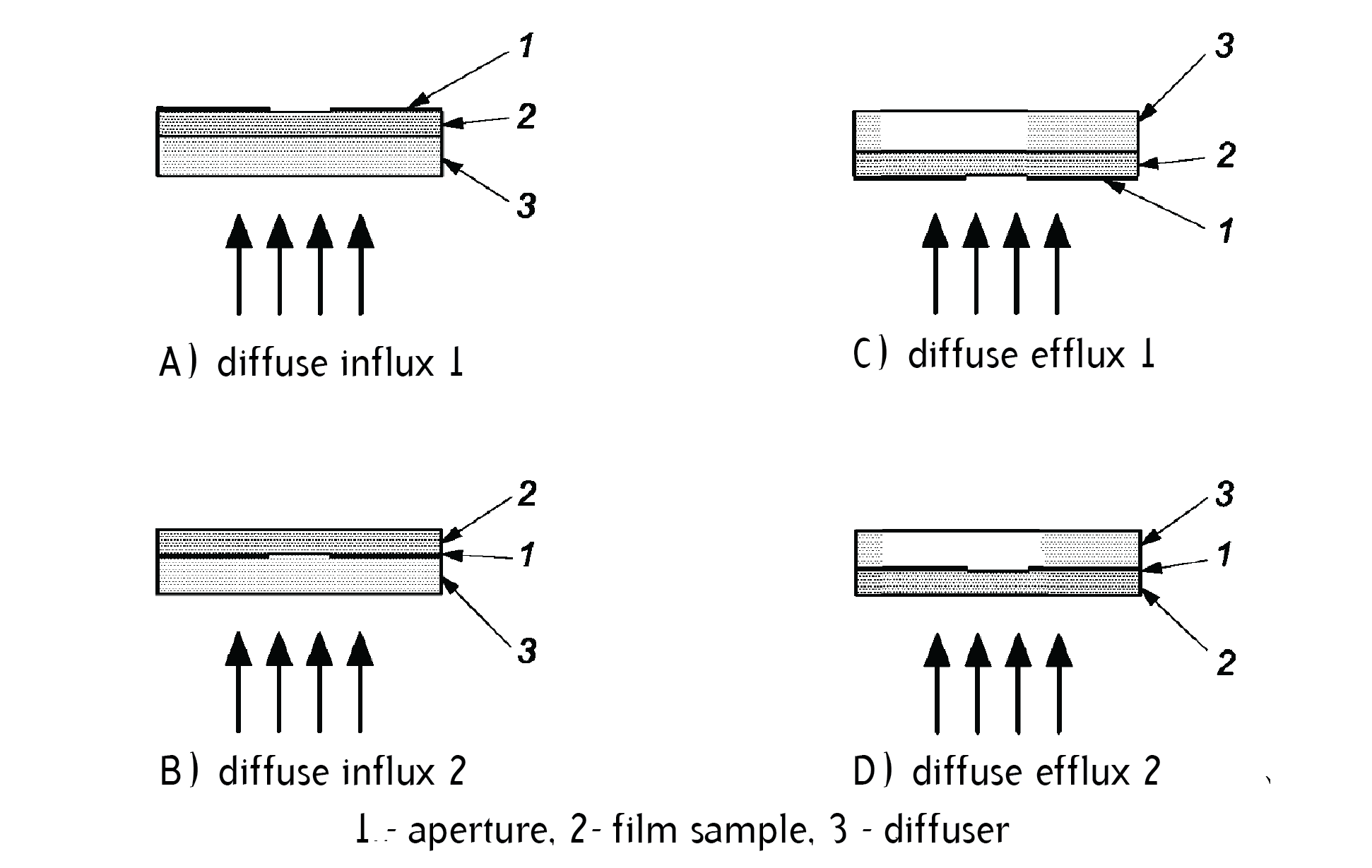
Truly a bombshell, I know. Basically, the standard defines the measurement geometry in terms of the solid angle of the incident and transmitted beams. So, what are the values for the half-angles kᵢ and kₜ, respectively? It depends. Historically, several combinations of incident and transmitted angles have been defined in the standard in order to specify density measurements for different applications. But for all intents and purposes, and in recent versions of the standard, one type of density rules supreme - diffuse density. In order to measure diffuse density kᵢ must equal 90° and kₜ must be 10° or vise versa… Let’s unpack the meaning of this - our incoming light beam must have a solid angle of 180°, i.e. the incident light rays should enter the sample at ALL angles - from perpendicular to barely grazing. Well, this is diffuse light! Our collection, or efflux, beam has a solid angle of only 20°. That is pretty focused, not entirely specular, but pretty close. The standard specifies that the geometries can be reversed, so we can use a focused incident beam of 20° and collect ALL the light passing through the sample.
For completeness’ sake, we can briefly consider the all combinations of influx and efflux beams and what they are called:
Designations of density when a focused beam is passed through a sample
Designations of density when diffuse light is transmitted through a sample
These designations are somewhat arbitrary and so are the angles associated with them, but they are sometimes referenced in literature, so I find it useful to know their meaning.
So, a diffuse densitometer passes diffuse light through a sample and collects a narrow efflux beam in order to measure density. What other photographic optical systems work in the same or similar way? Diffuser enlargers do. Contact printing ditto! In the former case, diffuse light passes through the negative and the outgoing beam is focused to the base of the enlarger. In the former, a focused beam of light (such as that from an enlarger or a point light source) is projected on a negative in contact with the photo paper, which thus will collect all the transmitted light. Thus, diffuse density has become universal, as it is applicable to the two most common types of printing.
Well, what about condenser enlargers? They shine a (somewhat) collimated light beam through the negative and focus it down to the print. Therefore, specular or semi-specular density is a more appropriate way to measure density when enlarging with a condenser. And indeed, there will be a difference - we know that condenser enlargers produce prints with a higher contrast. This is because of scattering - the silver grains in a negative emulsion not only absorb light, but they deflect its path and redirect it, somewhat like a diffuser. This scattering increases as the number of silver particles (or their density in the emulsion) increases. For contact printing, this scattering is not of much consequence. For projection printing, the scattering will have some effect, but since the unobstructed light entering the lens system from the source is by definition diffuse, the effect is not significant. But in a condenser system, as the density increases, more of the collimated light is redirected and lost, while nearly all of the collimated light that passes through the clear parts of a negative is transmitted onto the print. This is known as the Callier effect and the ratio between specular (or “projection”) and diffuse density is known as the Callier Q factor. Q grows rapidly for densities up to about 0.8-1 and then levels out around 1.4. It depends on the optical system of the enlarger, as well as the type of film, it’s grain size, the thickness of the emulsion, etc. In practice, this influence is offset by intentional and unintentional effects, so a practicing printer will probably never have to consider the Callier coefficient when evaluating a negative. Point-source condenser enlargers make use of the Callier effect to produce very sharp and high-contrast (both micro- and macro)prints.
Now, back on track - measuring density. Before reviewing reflection density and how its geometry is defined, let’s look back to the ISO standard and see how it helps us a bit further by describing practical implementations for transmission density measurement. It recommends that light diffusion is achieved through an opal or similar diffuser having a near-perfect cosine response (aka Lambertian distribution). This just describes how much light exists at what angle from a diffusing volume. For example, some diffusing materials may transmit too much light along the incident axis, i.e. they are not good enough diffusers! Finding a diffusing material which is good at redirecting light in a cosine response but also does not block too much light is a challenge and one that we will eventually face when designing our densitometer. One more practical element is described but not strictly prescribed in the standard - the shape and size of the area we will measure the density of. This hole or aperture is located on a mask that defines the sample area and blocks stray light form affecting our measurement. We will define out apertures when making practical considerations for our densitometer. Too big an area, and it will be difficult to find such large uniform areas of density on a negative to measure. Too small and we might have diffraction effects, or before that - begin picking up the granularity of the negative.
So, we know the influx and efflux angles and we can suppose that for our transmission densitometer we will need at least: a light source, a diffuser, the sample under test, and a light detector. The standard provides four configurations of these basic elements, which fulfill its requirements for the geometry:
These configurations imply that the aperture must always be in contact with the sample to be measured and then the diffuser can be either precede or follow them. This may sound and appear deceptively simple; but, let’s consider for a moment how NIST implements this in their standard transmission densitometer:
From my research, and reverse-engineering (which will be discussed in the next installment), I settled on the following measurement system for my densitometer:
Here, the light source can be either collimated or diffuse, the aperture plate ideally is also the mechanical support for the film and for the opal diffuser and the collection cone is a rudimentary lenseless projection system. Later on, I will show how this evolved into the current design, with its pros and cons.